Zum Inhalt

Simulation

Signal-Generatoren

Periodisch

Eine einfache periodische Funktion ist das Sinus-Signal, dass mit einem Rauschanteil überlagert wird.

\[ x(t) = sin( \omega \cdot t) + w(t) \\ w(t) = N(\sigma) \]

Das Skript zeigt einen "statischen" Aufbau:

sinusSignal.py 

# =============================================================================
# Sinus-Signal mit Rauschüberlagerung
# =============================================================================
import numpy as np
import matplotlib.pyplot as plt

# -----------------------------------------------------------------------------
# Parameter
n = 200
T1 = 1
T = 0.1

# Rauschsignal anlegen (Normalverteilung, n-Elemente, Amplitude=0.5)
w = np.random.randn(n)*0.5

# Speicher für Vektoren
t = np.linspace(0,100,n)
u1 = np.zeros(n)
u2 = np.zeros(n)
u = np.ones(n)
x = np.zeros(n)

# Signalerzeugung
for i in range(0,n):
    u[i] = np.cos(4*t[i]/100*np.pi)
    x[i] = w[i] + u[i]   


# Plot-Ausgabe ----------------------------------------------
plt.close('all')

fig = plt.figure(figsize=(5, 4))

ax1 = plt.subplot2grid((3, 4), (0, 0), colspan=2)
ax2 = plt.subplot2grid((3, 4), (0, 2), colspan=2)
ax3 = plt.subplot2grid((3, 4), (1, 1), colspan=2, rowspan=2)

ax1.plot(t,u, linewidth=3, color='#cc5200')
ax1.grid()
ax1.set_xlabel('$t/s$')
ax1.set_ylabel('$u(t)$')

ax2.plot(t,w)
ax2.grid()
ax2.set_xlabel('$t/s$')
ax2.set_ylabel('$w(t)$')

ax3.plot(t,x, linewidth=1)
ax3.plot(t,u, linewidth=2, color='#cc5200')
ax3.grid()
ax3.set_xlabel('$t/s$')
ax3.set_ylabel('$x(t)=u(t)+w(t)$')

plt.tight_layout()
plt.show()
Download: File

Stochastisch

Rauschen

Random Walk

Prozessmodelle

Musterprozess

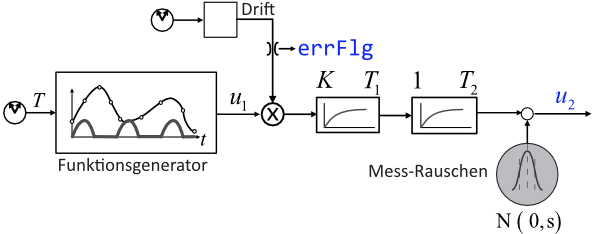
Der periodische Musterprozess soll eine die Signalkette mit Hilfe verschiedener standardisierter Einzelübertragungsblöcke demonstrieren. Mit diesem Konzept lassen sich sehr schnell individuelle signalbasierte dynamische Prozessmodelle entwickeln.

sequentielles Signalmodell

Die Signal-Pipeline besteht aus folgenden Blöcken:

  1. Taktgeber (erzeugt den Timestamp)
  2. Funktionsgenerator (hier: Amplitudenbegrenzte Sinus-Funktion)
  3. Drift-Generator, der überlagert wird (Multiplikation == Skalierung der Signal-Amplitude)
  4. Doppelte Verzögerung durch PT1-Glied
  5. Rauschanteil mit normalverteiltem Signal
sim__prozSig_plt_01.py 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
# -*- coding: utf-8 -*-
"""
@author: jbechtloff
Vorgabe: tsA, tsE, Timedelta

Zusammenführen von  sim_sig_design_03.py &
                    sim_mdb_struc_03.py
Generieren + Realtime                    
"""

import numpy as np
import pandas as pd
from PT1 import PT1

import matplotlib.pyplot as plt
plt.close('all')


class clProzess:
    def __init__(self,  T, T1, Kdrift, Tdrift, Kw):
        self.pt1a = PT1(T,T1)
        self.pt1b = PT1(T,T1)
        self.T = T
        self.Kdrift = Kdrift
        self.Tdrift = Tdrift
        self.Kw = Kw
        self.cnt = 0

    def simProz(self):
        k = self.cnt
        u_1 = np.sin(4*k/100*np.pi)
        if u_1 <0: u_1=0
        if u_1 > 0.5: u_1 = 0.5
        u_1 = u_1*2.0

        # Amplituden-Drift-Simu: 1.0 < u2 < 1.1 (MUL)
        a_Drift = 1.0 + self.Kdrift * (np.sin(4*k*self.T/self.Tdrift*np.pi)+1.0)/2.0
        errFl = 0
        if a_Drift > 1.0+19*self.Kdrift/20: errFl = 1.0
        u_2 = self.pt1b.PT1rek(self.pt1a.PT1rek(u_1*a_Drift))  # PT2-Verschleiß
        w = np.random.randn()*self.Kw

        self.cnt +=1
        return(u_1, u_2, a_Drift, w, errFl)

    def write_(self, ts):
        [u_1, u_2, a_Drift, wi, err_Flg] = self.simProz()

        data = {
            'ts': ts,
            'cnt': self.cnt,
            'u': u_2 + wi,
            'err': err_Flg
        }
        # print("%s" % (self.cnt))
        # print(data)
        return data


if __name__ == "__main__":

    Prozess = clProzess(T=1,T1=4,
                    Kdrift=0.1, 
                    Tdrift=2000, 
                    Kw=0.01)

    Tscal = {"s":1,"m":60,"h":60*60, "d":60*60*24}
    dT = 1
    dT_unit = "s"

    TsimSpan = 2
    TsimSpan_unit = "m"

    n = int(np.trunc(TsimSpan * Tscal[TsimSpan_unit] / (dT*Tscal[dT_unit])))

    vU = []
    vTS = []
    vErr = []

    # tsA = pd.Timestamp(2021,11, 20,  0,0,0)
    # tsE = pd.Timestamp(2021,11, 21,  10,0,0)
    # tsDeltaAE = tsE - tsA

    tsE = pd.Timestamp.now()        # now
    tsA = tsE - pd.Timedelta(TsimSpan,TsimSpan_unit) # Vorlauf

    ts = tsA
    while ts <= tsE: 
        data = Prozess.write_(ts)
        ts = ts + pd.Timedelta(dT,dT_unit)
        vU.append(data["u"])
        # vTS[data["cnt"]] = ts
        vTS.append(ts)
        vErr.append(data["err"])



    # Plot-Ausgabe -----------------------------------------

fig = plt.figure(figsize=(5, 4))
# df_F.plot(x="ts",y="u")

# matplotlib auf pd.Datetime einstellen

plt.plot(vTS,vU)
plt.plot(vTS,vErr,color='#FF0000')
plt.show()
Download: File

sim

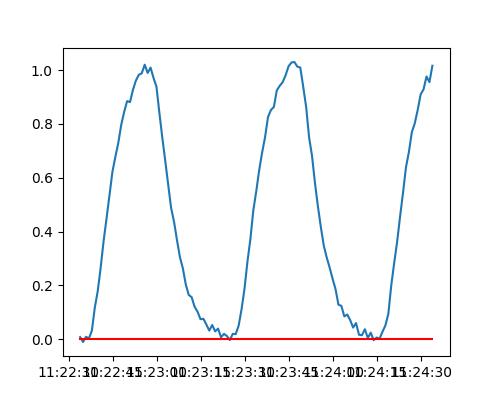
Simulationsergebnis als Plot-Ausgabe (tSim = 2m)

sim

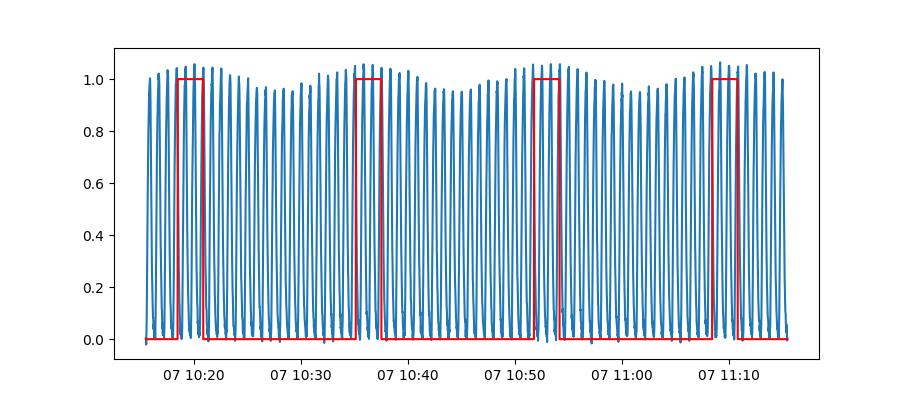
Simulationsergebnis als Plot-Ausgabe (tSim = 1h)

Info

Dieses Modell wird im Kapitel "Beispiel-Prozesse" eingesetzt.

Echtzeit-Simulation

APScheduler

"P:\docs_DNL\PY-simProz_mDB_NR\sim__prozSig_plt_01.py"