Simulation

Zentrale Frage

bei der Umsetzung einer IoT-Lösung:

"Wie kann während der Entwicklung getestet werden?"

Eng mit dieser Frage verknüpft ist dann die Frage nach dem Prozessmodell. Die Prozessmodellierung ist eine Grundaufgabe in den Ingenieurwissenschaften. In dieser Lehrunterlage wurden ja bereits eine ganze Reihe von Prozessmodellen zum Thema „Datenanalyse“ vorgestellt. Um eine Simulation für die Softwareentwicklung hinsichtlich der Aufgaben von a) IoT-Gateway und b) IoT-Plattform entwerfen zu können, müssen Fragen wie • Welche Detaillierung des physikalischen Modells ist erforderlich? • Wie kann die Simulation mit einem realen Prozess abgeglichen werden? • Auf welcher Grundlage wird ein Modell erzeugt? • Wieviel Aufwand entsteht bei der Modellbildung? • Wie ist ein Simulationsumfeld aufzubauen?

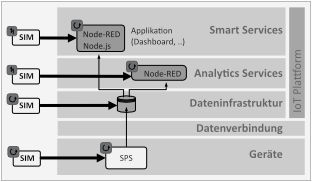
Allgemeines Konzept zur Einbindung von Simulationen entlang der IoT-Plattform-Architektur

Neben dem Eingriff in den Datenfluss spielt der Zoom-Faktor auf die zu simulierenden Systeme eine Rolle:

a) Wird der Strom im Antrieb einer Fügevorrichtung betrachtet? $$ T<<10 \rm{ms} $$

b) Wird die Folge von Arbeitsschritten beobachtet? $$ T ≈ 1 \rm{s} $$

c) Wird der Materialfluss mehrerer verketteter Maschinen beobachtet? $$ T ≈ 1 \rm{min} $$

d) Haupt-, Neben- und Stillstandszeiten mehrerer Produktionslinien beobachtet? $$ T ≈ 10 \rm{min} $$

Aus der Zeitskalierung (hier: Abtastzeit \(T\)) leiten sich die Algorithmen zur Signalgenerierung ab.