Simulationsmodell

Mit dem Modell eines Batch-Prozesses kommt aus der Verfahrenstechnik. Dort werden diskontinuierliche Chargen- oder Stapelprozesse eingesetzt, um z.B. chemische Reaktionen kontrolliert ablaufen zulassen. Der Prozess wird periodisch wiederholt. Fasst man das Prozessverständniss allgemeiner, dann lassen sich eine Vielzahl von technischen Produktionsprozessen als peridische Batch-Prozesse modellieren.

Neben der ideellen Zeitfunktion treten in der realen Produktionswelt zahlreiche Störeinflüssen auf: - Variation der Reaktionszeiten bzw. Ablauf-Zeitspannen - Variation von Prozessgrößen - Rauschsignal-Überlagerungen - Driften - ...

Zur Modellierung dieser Einflussgrößen können stochastiasche Teilmodelle eingesetzt werden.

Lineare Interpolation

Zwischen Stützstellen werden die Zwischenwerte linear berechnet. Es werden n Stützzstellen vorgegeben, die streng Monton angeordnet sein müssen. Gegeben sind zwei Datenpukte $(t_i, x_i)$ und $(t_{i+1}, x_{i+1})$ , die durch eine Strecke miteinander verbunden werden:

$x(t) = x_i + \frac { x_{i+1} - x_i } { x_{i+1} - x_i } (x - x_i)$

Gegeben ist eine Folge von Punkten: $$ [t_i, x_i], i=0(1)n $$

Die Vorgabe der Zeitabschnitte erfolgt abschnittsweise: $$t_i = t_{i-1} + \Delta t_i $$

Beispiele:

dt = [0, 10, 30,   43.2, 100, 120]
 x = [0,  0, 3.2,   8.2,   5,   0]

Stochastik

Die verschiedenen Werte sowohl bezogen auf die Zeitachse als auch auf die Werteachse können in Realprozessen variieren. Dieses Veränderungsverhalten wird in diesem Simulationsmodell stochastisch - also zufallsgesteuert - modelliert. Als Verteilungen kommen eine Gleichverteilung, eine Normalverteilung oder andere in Frage. Die meisten Produktionsprozessen verhalten sich in ihren Schwankungen normalverteilt.

Normalverteilung und ihre Parameter

Die Gaußsche Normalvertielung

$h(x) = \frac 1 {\sqrt{2 \pi \sigma ^2}} \cdot e ^ { \frac {(x - \mu)^2} {2 \sigma^2}}$

wird mit den Parametern - $\mu$ == Mittelwert - $\sigma$ == Standardabweichung

beschrieben. Die resultierende Häufigkeitsverteilung zeigt das nachfolgende Bild:

Unter Vorgabe der Streubreite $\sigma$ lassen sich Zahlen generieren, die zu 68,3 % innerhalb des Bereichs $\pm \sigma$ liegen.

Dieser Ansatz wird nun auf die Vorgabe des Batchprozesses angewendet. Amplitudenvorgaben können um $x_i = \hat{x}_i \pm \sigma$ zufällig variieren, Zeitangaben hingegen sollen nur "Länger" werden können $t_i = \hat{t}_i + |\sigma$ |.

Die Vorgabe einer Batch-Zeitreihe sieht nun so aus:

# Zeitabschnitte ==Differenzen, erster Wert = 0 !
dt =    [0, 10, 20, 50, 60]
# Sigma (erster Wert =0)
tSig =  [0, 50.01, 0.05, 0.06, 0.1]

[[bat]]
# Amplitudenwerte
x =     [0, 0, 50, 50, 0]
# Rauschanteil (pro Durchlauf)
xSig =  [0.001, 0.001, 0.005, 5, 0.002]

Signalmodell

Der Gesamtverlauf wird nun mittels eines Messrauschen und einem Regelkreis, bestehnd aus dem Regler $F_R(s)$ PI-Regler und der zu regelnden Strecke $F_S(s)$ als PT1-Strecke weiter an realen Prozesssignale angepasst. Der Signalflussplan erklärt die Signalverarbeitung:

Das Regelkreisverhalten mit $T_N = T_1$ kann mit einem PT1-Glied Verzögerungsverhalten 1. Ordnung vereinfacht werden, so dass als resultierender Modellparameter T1 verbleibt:

Damit sind zwei weitere Parameter für die Batch-Prozess-Simulation einzuführen:

w  =  1   # Messrauschen
T1 =  1   # PT1-Filter-Zeitkonstante

Beispiele

Brennofen

Bei einem Brennofen - z.B. für Keramik-Erzeugnisse - ist genau das oben gezeigte Prozessführungsprofil erforderlich.

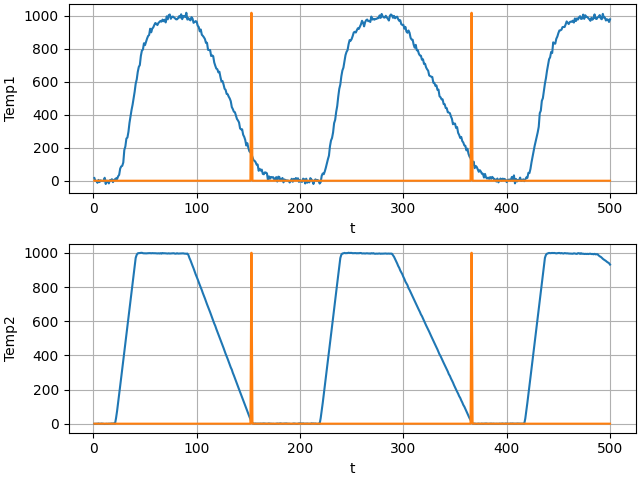
Die zugehörige toml-Konfigurationsdatei Download:

BrennProz.toml

# Abstastzeit in sec.
T = 1

# Zeitabschnitte == Differenzen, erster Wert = 0 !
dt =    [0, 10, 20, 50, 60]
# Sigma (erster Wert =0)
tSig =  [0, 50.01, 0.05, 0.06, 100]

[[bat]]
# Amplitudenwerte
x =     [0, 0, 1000, 1000, 0]
# Rauschanteil (pro Durchlauf)
xSig =  [0.001, 0.001, 0.005, 0.002, 0.002]
w =     10   # Messrauschen
T1 =    10   # PT1-Filter-Zeitkonstante
name = "Temp1"   # Name der Größe
[bat.meta]
unit = "°C"
min = 0
max = 1200

[[bat]]
# Amplitudenwerte
x =     [0, 0, 1000, 1000, 0]
# Rauschanteil (pro Durchlauf)
xSig =  [0.001, 0.001, 0.005, 5, 0.002]
w =     1   # Messrauschen
T1 =    1   # PT1-Filter-Zeitkonstante
name = "Temp2"   # Name der Größe
[bat.meta]
unit = "°C"
min = 0
max = 1200

Kunststoffspritzgießen

todo

Trest-Zeile

Test Nchsteeile